At long last, my job application is done.
The file contains CV, research and teaching statements. If you're in a research lab, ignore any mention of how I like to teach ;)
Wednesday, December 19, 2007
Monday, December 17, 2007
Travel pictures (2): Kakamega Rainforest
Look at me, I can fly!

Pensative blue monkey:

Another blue monkey:

The eternal fight for food (the monkey climbed on Mira, bit her hand, and got the banana -- but I didn't quite have time to set up for the photo):

Black and white Colobus monkey:
 The red-tail monkey:
The red-tail monkey:

Romanians are close descendents of monkeys:


I have a big telelens:

Many many ants:


Pensative blue monkey:

Another blue monkey:

The eternal fight for food (the monkey climbed on Mira, bit her hand, and got the banana -- but I didn't quite have time to set up for the photo):

Black and white Colobus monkey:
 The red-tail monkey:
The red-tail monkey:
Romanians are close descendents of monkeys:


I have a big telelens:

Many many ants:

Travel pictures (1): Kenya life
The dead was a rich man, he could afford a coffin. (I am told poor people pick their dead from the hospital wrapped in a mattress).

I live in the Romanian hut on the volunteer camp:

The medical clinic, and "the mobile clinic" (the van):
Inside the clinic: Dr. Mira and assisting clinical officer Belinda.

Medicine, Kenyan style (writing on the first jug: "Paracetamol")

On most days, the mobile clinic travels to remote villages to see people there. They set up in local churces, such as the following Catholic church:

If they are lucky, the curch has a separate room which becomes "the examination room":


I live in the Romanian hut on the volunteer camp:

The medical clinic, and "the mobile clinic" (the van):

Inside the clinic: Dr. Mira and assisting clinical officer Belinda.

Medicine, Kenyan style (writing on the first jug: "Paracetamol")

On most days, the mobile clinic travels to remote villages to see people there. They set up in local churces, such as the following Catholic church:

If they are lucky, the curch has a separate room which becomes "the examination room":

Monday, December 10, 2007
Non-post
I made it to the Internet in town after a 10km walk. As Piotr had so wisely predicted, I am now a bit tired and not really feeling like writing a blog post. :)
Instead, let me point you to a recent comment by Kamal Jain (addressing my post about his talk), which is long enough to serve as a blogpost in itself :) Reply on that thread if you want to say something.
Instead, let me point you to a recent comment by Kamal Jain (addressing my post about his talk), which is long enough to serve as a blogpost in itself :) Reply on that thread if you want to say something.
Thursday, December 6, 2007
Away
An excellent tradition in the US academic world is the sabbatical: roughly every 6 years, you take a year off (with some pay). People typically travel around the world, spend some time at other universities, interact with industry etc. I think this is a great idea for maintaining your creativity and breadth, and it's a shame that companies which require serious thinking don't have a similar benefit.
In my own case, I have started doing research about 5 and a half years ago. And, the eager person that I am, I decided to take a sabbatical a bit early. Of course, since I'm still on MIT's payroll as a student, this is a bit unofficial :) But the basic idea is the same.
This is mostly plan-as-you-go, but here's the rough idea:
My main goals on this trip are to (1) relax and enjoy the life experience, (2) think about some really long-shot problems, (3) think about some diverse fields of research that I have not considered before. I feel a great danger for researchers is to get stuck improving a field that they have revolutionized earlier. One needs to spend time targeted at starting new revolutions, not on your old business-as-usual research.
So, going with the plan, I have spent the past week in London, minding the gap and trying not to get killed by all those maniacs driving on the wrong side of the road. (This skill proves useful, since they are also at it in Kenya.) London is a nice city, but I feel it has lost some of the European charm that I find in many cities on the continent. Or maybe I'm desensitized by prolonged exposure to American culture, a close descendant of the British culture.
The most durable thing about visiting London is the hole in your wallet. Roughly speaking, all prices look like the right number, except that they have this funny pound sign instead of "$". With an exchange rate of $2.2 for a pound, it feels like your pay-check comes from a third-world country. Unfortunately, dark days seem to lie ahead for all of us relying on this collapsing economy...
Today, I am in Nairobi catching up with things, and tomorrow I will be enjoying a 9-hour bus ride to the other end of Kenya. I will try to post once in a while depending on Internet connectivity (they say there's a post office with an Internet connection, at a convenient 10-mile run). But of course, if I happen to solve P vs NP I will make an effort to post about it.
In my own case, I have started doing research about 5 and a half years ago. And, the eager person that I am, I decided to take a sabbatical a bit early. Of course, since I'm still on MIT's payroll as a student, this is a bit unofficial :) But the basic idea is the same.
This is mostly plan-as-you-go, but here's the rough idea:
- first week of December: London.
- 6 weeks in a rural location in East Kenya, with a small detour to do white-water rafting in Uganda (at the source of the Nile)
- 1+ weeks climbing Kilimanjaro and taking a safari (Tanzania).
- 3 weeks in Romania (yes, I will gladly give talks!)
- 1 week in Dagstuhl (session on data structures)
My main goals on this trip are to (1) relax and enjoy the life experience, (2) think about some really long-shot problems, (3) think about some diverse fields of research that I have not considered before. I feel a great danger for researchers is to get stuck improving a field that they have revolutionized earlier. One needs to spend time targeted at starting new revolutions, not on your old business-as-usual research.
So, going with the plan, I have spent the past week in London, minding the gap and trying not to get killed by all those maniacs driving on the wrong side of the road. (This skill proves useful, since they are also at it in Kenya.) London is a nice city, but I feel it has lost some of the European charm that I find in many cities on the continent. Or maybe I'm desensitized by prolonged exposure to American culture, a close descendant of the British culture.
The most durable thing about visiting London is the hole in your wallet. Roughly speaking, all prices look like the right number, except that they have this funny pound sign instead of "$". With an exchange rate of $2.2 for a pound, it feels like your pay-check comes from a third-world country. Unfortunately, dark days seem to lie ahead for all of us relying on this collapsing economy...
Today, I am in Nairobi catching up with things, and tomorrow I will be enjoying a 9-hour bus ride to the other end of Kenya. I will try to post once in a while depending on Internet connectivity (they say there's a post office with an Internet connection, at a convenient 10-mile run). But of course, if I happen to solve P vs NP I will make an effort to post about it.
Monday, November 26, 2007
Theory Channel Line-up
Via Muthu, I hear about the Aggregator. Here's the deal: most people use RSS readers (which they should be, for example reader.google.com is wonderfully easy to use). But if you're among those people who deliberately avoid readers, you find yourself navigating to all the webpages for various blogs. The aggregator can save you some clicks, by merging all Theory CS blogs into one page. So if you're a theorist and reader-hater, bookmark this page.
PS: Yes, the picture of me on this site (left side below) has great nostalgic value. But a few restless years later, I look more like on the right side...
 May'04 ---??--> Oct'07
May'04 ---??--> Oct'07 
PS: Yes, the picture of me on this site (left side below) has great nostalgic value. But a few restless years later, I look more like on the right side...
 May'04 ---??--> Oct'07
May'04 ---??--> Oct'07 
Sunday, November 25, 2007
Death to intellectuals
Ion Iliescu, former president of Romania (1990-1996, 2000-2004), now has a blog. Of course, after the ever ridiculous Mahmoud Ahmadinejad got his blog, this may not sound so shocking. But, trust me, this 77-year old Romanian blogger really is special.
To my international readers: if some stories (in particular, the miner story) seem just too much to be true, let me assure you -- they are entirely true, and accepted history.
Communist years. Iliescu got his political training in Moscow during the first years of Romanian communism, and compensated for being homesick by contributing editorials to the Romanian state-run newspaper (Scânteia) . The topic was of course the contrast between the primitive capitalist imperialist cannibals, and the new glorious communist society.
Back to Romania, he quickly advanced in the nomenclatura to be a minister. In the 70s he was seen by everybody as Ceauşescu's heir, which began to freak out the dictator. As a result, Iliescu was sent to be prime secretary in various remote counties.

The revolution. The Romanian revolution is a unique event in European history. Unlike the velvet revolutions in other communist countries, this one was not about throwing three stones and breaking two windows: at the end, more than 1100 people were dead, and 3300 wounded. We know who these people are: demonstrators who were assailing government buildings. But unlike other bloody conflicts in recent memory, we have no idea who shot these people and why. The official reports indicated that "unidentified terrorists shot the demonstrators." (rather sensitive choice of a word, isn't it?)
One must find it truly remarkable that to this day we have no plausible explanation. In similar cases, we always have a very plausible official version (say, Bin Laden), which conspiracy theorists choose not to believe. Personally, I seldom count myself among conspiracy theorists, but faced with the lack of an explanation, I have to become one.
Many (most?) Romanians have suspected that Iliescu and other leading party members seized the opportunity of public unrest to stage a revolution, and seize power. The secret service was ordered to shoot enough people to make the revolution credible, without actually stopping the demonstrators. NB: it seems clear that a militaristic communist state had enough bullets, grenades and tanks to keep demonstrators out of the presidential palace, especially with several days' notice.
Conspiracy theory aside, the fact is that high-ranking communist officials, led by Iliescu, emerged as leaders of the anti-communist struggle (!!), and obtained control of "revolutionary party." In the days after the revolution, Iliescu was an inspiration to democracy fighters with statements like:
The authorities (aka the revolutionary party) turned the propaganda machine against the demonstrators, aided of course by control of the media. On some days, Iliescu would call the demonstrators worthless hooligans, who might as well remain on the streets. On other days, the demonstrators were fascists, probably infiltrators from the West. A remarkable quote by another leading party member (Brucan) was "Of course we will not talk to them; how can you talk to someone who doesn't eat? My only advice is that they should have a steak."
The response of the demonstrators was to proudly adopt the name hooligans (esp. in the Romanian form golani). A song of those days, which over the years has gained moving overtones, proclaimed that "I'd rather be a hooligan, than a party activist/ I'd rather be dead, than again communist." Song on YouTube.
Miners. Unable to address the Piaţa problem, Iliescu decided to take drastic measures: he called the miners from the Petroşani region to "protect the democracy." Armed with identical fighting clubs and a mob mentality, some 12000 miners boarded special trains for Bucharest. Stopping briefly in Craiova (where I lived), they managed to trash a neighborhood in half an hour, with apparently no good reason.
Reaching Bucharest, they immediately attacked the demonstrators, shouting two infamous slogans:
That night, students wrote on the university wall adjacent to the square "TianAnMen II."
In the following days, the miners roamed the streets looking for potential revolutionaries (i.e. beating up people with a beard or long hair). To encourage democracy, they also trashed all opposition parties, making a famous report that they had found intoxicating drugs that the opposition was going to use to influence voters, capitalist propaganda materials, "and a typewriter."
At the end, Iliescu came down among the miners and (in a live broadcast on national TV) thanked the miners "for being a strong force, one with an attitude of high civic conscience."
Years later, Iliescu denied that he had anything to do with the violent actions of the miners. In another remarkable quote, he said "I had called the miners to plant pansies in university square" (să planteze panseluţe) after the demonstrators retreated.
Here is a video capturing key moments of those days. It should make sense even if you don't speak Romanian.
Then, Mr. Former President, I can only suggest that you decorate your new blog with pansies. Welcome to the blogosphere, where I can assure you that your feelings towards the intellectuals are entirely reciprocated.
To my international readers: if some stories (in particular, the miner story) seem just too much to be true, let me assure you -- they are entirely true, and accepted history.
Communist years. Iliescu got his political training in Moscow during the first years of Romanian communism, and compensated for being homesick by contributing editorials to the Romanian state-run newspaper (Scânteia) . The topic was of course the contrast between the primitive capitalist imperialist cannibals, and the new glorious communist society.
Back to Romania, he quickly advanced in the nomenclatura to be a minister. In the 70s he was seen by everybody as Ceauşescu's heir, which began to freak out the dictator. As a result, Iliescu was sent to be prime secretary in various remote counties.

The revolution. The Romanian revolution is a unique event in European history. Unlike the velvet revolutions in other communist countries, this one was not about throwing three stones and breaking two windows: at the end, more than 1100 people were dead, and 3300 wounded. We know who these people are: demonstrators who were assailing government buildings. But unlike other bloody conflicts in recent memory, we have no idea who shot these people and why. The official reports indicated that "unidentified terrorists shot the demonstrators." (rather sensitive choice of a word, isn't it?)
One must find it truly remarkable that to this day we have no plausible explanation. In similar cases, we always have a very plausible official version (say, Bin Laden), which conspiracy theorists choose not to believe. Personally, I seldom count myself among conspiracy theorists, but faced with the lack of an explanation, I have to become one.
Many (most?) Romanians have suspected that Iliescu and other leading party members seized the opportunity of public unrest to stage a revolution, and seize power. The secret service was ordered to shoot enough people to make the revolution credible, without actually stopping the demonstrators. NB: it seems clear that a militaristic communist state had enough bullets, grenades and tanks to keep demonstrators out of the presidential palace, especially with several days' notice.
Conspiracy theory aside, the fact is that high-ranking communist officials, led by Iliescu, emerged as leaders of the anti-communist struggle (!!), and obtained control of "revolutionary party." In the days after the revolution, Iliescu was an inspiration to democracy fighters with statements like:
- Let's build a Communism with a humane face! (eternul "comunism cu o faţă umană")
- Ceauşescu tarnished the noble ideals of Communism ("a întinat nobilele idealuri")
- The multi-party system is a backwards concept ("sistem retrograd")
The authorities (aka the revolutionary party) turned the propaganda machine against the demonstrators, aided of course by control of the media. On some days, Iliescu would call the demonstrators worthless hooligans, who might as well remain on the streets. On other days, the demonstrators were fascists, probably infiltrators from the West. A remarkable quote by another leading party member (Brucan) was "Of course we will not talk to them; how can you talk to someone who doesn't eat? My only advice is that they should have a steak."
The response of the demonstrators was to proudly adopt the name hooligans (esp. in the Romanian form golani). A song of those days, which over the years has gained moving overtones, proclaimed that "I'd rather be a hooligan, than a party activist/ I'd rather be dead, than again communist." Song on YouTube.
Miners. Unable to address the Piaţa problem, Iliescu decided to take drastic measures: he called the miners from the Petroşani region to "protect the democracy." Armed with identical fighting clubs and a mob mentality, some 12000 miners boarded special trains for Bucharest. Stopping briefly in Craiova (where I lived), they managed to trash a neighborhood in half an hour, with apparently no good reason.
Reaching Bucharest, they immediately attacked the demonstrators, shouting two infamous slogans:
- Death to intellectuals! (Moarte intelectualilor)
- We work, we don't think! (Noi muncim, nu gândim) -- in line with the standard communist doctrine that the working class is the only legitimate ruler of a country.
That night, students wrote on the university wall adjacent to the square "TianAnMen II."
In the following days, the miners roamed the streets looking for potential revolutionaries (i.e. beating up people with a beard or long hair). To encourage democracy, they also trashed all opposition parties, making a famous report that they had found intoxicating drugs that the opposition was going to use to influence voters, capitalist propaganda materials, "and a typewriter."
At the end, Iliescu came down among the miners and (in a live broadcast on national TV) thanked the miners "for being a strong force, one with an attitude of high civic conscience."
Years later, Iliescu denied that he had anything to do with the violent actions of the miners. In another remarkable quote, he said "I had called the miners to plant pansies in university square" (să planteze panseluţe) after the demonstrators retreated.
Here is a video capturing key moments of those days. It should make sense even if you don't speak Romanian.
Then, Mr. Former President, I can only suggest that you decorate your new blog with pansies. Welcome to the blogosphere, where I can assure you that your feelings towards the intellectuals are entirely reciprocated.
Friday, November 16, 2007
Good Friday
To: coauthor-1. Sorry, I am a bit delayed due to another paper, and I still don't have a complete draft, but the paper is falling nicely into place. I promise to have a first draft out by Monday morning.
~/work% mkdir 4D
~/work$ cp ~/bs/preamble.tex 4D/paper.tex
~/work$ cp ~/bs/hacked-article.cls 4D/article.cls
~/work$ cp ~/bs/hacked-size11.clo 4D/size11.clo
TODO:
- title?
- abstract
- intro. Track down fractional cascading refs!
- figure out complete list of coauthors
- figure out how to analyze Bob's side of the rectangle (NB: we're losing smthg like a log or log^2 in the density of queries, is the intuition still true?)
- technical section
- make nice drawing with 2 coupled trees
- does a 2-sided lb seem doable? Figure out whether to claim it "in the full version".
- announce social event Monday 4am, G575. Buy cookies for event.
- confirm postdeadline beer @CBC, 8:30pm.
Tuesday, November 13, 2007
Is Google paying you?
Kamal Jain gave a talk today on "atomic economics". Here is my own description of what he meant, though it seemed Kamal disagrees with at least some of my description :)
Think of credit cards. Whenever I pay with one, the store only gets 1-x% of the posted price, i.e. the the credit card company makes x% of the money. That is nice profit for the CC company, but as always, competition is driving all profits towards zero. Since there are multiple banks willing to give me a CC, and they all retain the same percentage from a merchant, they need to compete on the customer side --- they have to fight for the honor of counting me as their customer. So they start giving me points / miles / cash back / etc. Getting 1% of your money back is already quite standard, and customers need more to be impressed. To some extent, this incentivizing actually works (personally, I tend to use my AmEx card due to the better reward system).
Now, Google and Yahoo are making money because of me (merchants pay them when I click on an ad). In principle, this means we are not at an equilibrium: since these companies are competing for customers (equal ad revenue), one of them should start offering me a share of their profits whenever I click, and the other will have to follow suit.
Kamal sees several problems (market inefficiencies) that will prevent this welfare-maximizing scenario. I also see them as problems, but I have a different opinion on the degree of surmontability. Problems:
The market inefficiency generated by the small scale of Web transactions is great for Web-based companies like Google, since it means they can make huge profits below the radar of competition forces. The sad news (for a scientist) is that it all becomes a social competition, instead of a scientific/economic one. It's much more important if I, the customer, like Google's colors than if I'm getting my fair share of cash back.
On a larger scale, is this a social problem? I guess so, but not a very big one. If our threshold for irrationality is below 1%, the total income of such companies cannot grow above 1% of the money we all spend. But we're already paying the Federal government some 30% of what we make, and quite possibly many of us are happier with the success of Gmail than the hearts-and-minds campaign in Iraq.
PS: Given the topic, the number of jokes and anecdotes in Kamal's talk was too small by an order of magnitude. This reinforces my belief that we shouldn't be doing this kind of thing (i.e. study pure economics, because it is has something to do with networks or computers). If such pursuits will be more than wasted theoretical brain-cycles, they need to impact managers and policy-makers. But for that to happen, we need to give talks at the level of political speeches, and no self-respecting theorist is willing to do that. People in economics (who incidentally serve on policy-making boards every now and then) have already developed the art of communicating to politicians.
Think of credit cards. Whenever I pay with one, the store only gets 1-x% of the posted price, i.e. the the credit card company makes x% of the money. That is nice profit for the CC company, but as always, competition is driving all profits towards zero. Since there are multiple banks willing to give me a CC, and they all retain the same percentage from a merchant, they need to compete on the customer side --- they have to fight for the honor of counting me as their customer. So they start giving me points / miles / cash back / etc. Getting 1% of your money back is already quite standard, and customers need more to be impressed. To some extent, this incentivizing actually works (personally, I tend to use my AmEx card due to the better reward system).
Now, Google and Yahoo are making money because of me (merchants pay them when I click on an ad). In principle, this means we are not at an equilibrium: since these companies are competing for customers (equal ad revenue), one of them should start offering me a share of their profits whenever I click, and the other will have to follow suit.
Kamal sees several problems (market inefficiencies) that will prevent this welfare-maximizing scenario. I also see them as problems, but I have a different opinion on the degree of surmontability. Problems:
- Customer abuse: profit sharing has to be tied to some actual buying event, or otherwise I will have an incentive to spend my day clicking on ads (and not buying anything), driving the merchant out of business. This is a problem for branding ads (e.g. eBay likes to display worthless ads all the time to build its name into collective conscience), and for ads that are separated from the actual purchase (e.g. an ad to a restaurant). But for e-commerce, which seems to be the raison d'etre of search advertising, this detail can be worked out by sharing information between Google and the merchant.
- Merchant fraud: the merchant marks the price up by $5, adds $5 to the advertising budget (getting a top slot), and tells me that I will get $5 cash-back from Google (which means I don't care their price was $5 higher than the competition). Realistically, this won't happen, for several well-understood reasons. Common sense dictates that Google will only share a percentage of their profit, so I'll only get, say, $2.5 back, which means I care about the price markup. Like credit-card companies, Google and Yahoo have a weapon to enforce this common sense: customer differentiation. This is oligopolistic behavior, but one that is remarkably stable. What happens is that frequent buyers (resp. people with good credit histories) get better cash-bask deals, because they are presumed to have more authority to "negotiate". Then, the merchant gets a mix of people with different cash-back percentages, but who look the same to the merchant.
- Bounded rationality, a heavily used buzzword, and the really exciting consideration. Unlike traditional advertising, Google and Yahoo have really tiny costs. This means they can still make a ton of money with a razor-thin cut of the merchant's profit. For instance, if Google is paid 0.1% percent of the transaction value, what could they offer me as an incentive? Maybe 0.05% of the price. But that will be irrelevant to me -- the mental cost of remembering that Google gives me more cash back on lingerie gifts vastly outweighs the 0.05% payoff.
The market inefficiency generated by the small scale of Web transactions is great for Web-based companies like Google, since it means they can make huge profits below the radar of competition forces. The sad news (for a scientist) is that it all becomes a social competition, instead of a scientific/economic one. It's much more important if I, the customer, like Google's colors than if I'm getting my fair share of cash back.
On a larger scale, is this a social problem? I guess so, but not a very big one. If our threshold for irrationality is below 1%, the total income of such companies cannot grow above 1% of the money we all spend. But we're already paying the Federal government some 30% of what we make, and quite possibly many of us are happier with the success of Gmail than the hearts-and-minds campaign in Iraq.
PS: Given the topic, the number of jokes and anecdotes in Kamal's talk was too small by an order of magnitude. This reinforces my belief that we shouldn't be doing this kind of thing (i.e. study pure economics, because it is has something to do with networks or computers). If such pursuits will be more than wasted theoretical brain-cycles, they need to impact managers and policy-makers. But for that to happen, we need to give talks at the level of political speeches, and no self-respecting theorist is willing to do that. People in economics (who incidentally serve on policy-making boards every now and then) have already developed the art of communicating to politicians.
Friday, November 9, 2007
Branding and STOC/FOCS
Kamal Jain gives some advice on resubmitting papers that got rejected from STOC/FOCS. That reminds me of a question I've had for while: can you build up a name by only submitting papers in the right places (i.e. where they get accepted)?
Personally, I feel very strongly about self-selection. In my (short) career, I have had a total of 2 rejects:
Is this advice short-sighted? Does having a low reject rate help you in getting more attention from reviewers? If a reviewer knows you're not a "deceiver", he will feel uneasy about rejecting, and will think about it for another minute -- at the very least, he knows one person in the world (you, the author) finds the paper interesting. If a reveiwer has already rejected a couple of your papers, he won't have so many moral problems -- after all, it's possible that you yourself don't think the paper is good enough.
What do you think? Can you get reviewer sympathy by active self-selection?
Personally, I feel very strongly about self-selection. In my (short) career, I have had a total of 2 rejects:
- a paper rejected from ICALP, which got accepted to the subsequent SODA ;)
- a "short paper" rejected from SODA, which essentially disappeared (we came up with new ideas and obtained much better results). Incidentally, I'm glad the short track at SODA was stopped. It was a temptation to do mediocre work -- if you write a really good result in 2 pages, you will always get accepted even without the short track.
Is this advice short-sighted? Does having a low reject rate help you in getting more attention from reviewers? If a reviewer knows you're not a "deceiver", he will feel uneasy about rejecting, and will think about it for another minute -- at the very least, he knows one person in the world (you, the author) finds the paper interesting. If a reveiwer has already rejected a couple of your papers, he won't have so many moral problems -- after all, it's possible that you yourself don't think the paper is good enough.
What do you think? Can you get reviewer sympathy by active self-selection?
Tuesday, November 6, 2007
Cute Problem: Wooden Convex Hull
I didn't manage to keep an earlier promise to post olympiad-style problems... But here is a cute one.
You have n trees at given coordinates in the plane. You want to build a polygonal fence around the trees. However, the only way to get wood for the fence is to cut down some trees in the first place! Let's say each tree gives you enough wood for M meters of fence. The goal is to find the minimum k, such that you can cut down some k trees, and surround the rest by a fence of M*k meters.
What is the best algorithm you can find? Express your answer in terms on n and k.
As a bonus challenge, find a fast algorithm for the case when trees give you a different amount of wood M1, ..., Mi.
You have n trees at given coordinates in the plane. You want to build a polygonal fence around the trees. However, the only way to get wood for the fence is to cut down some trees in the first place! Let's say each tree gives you enough wood for M meters of fence. The goal is to find the minimum k, such that you can cut down some k trees, and surround the rest by a fence of M*k meters.
What is the best algorithm you can find? Express your answer in terms on n and k.
As a bonus challenge, find a fast algorithm for the case when trees give you a different amount of wood M1, ..., Mi.
Monday, November 5, 2007
Napkins
The inexhaustible Muthu came up with the fantastic idea of assembling napkins used for research-related work. This could turn out to be very interesting.
Here is my own contribution: a Starbucks napkin filled during a 2 hour caffeinated discussion with Alex. It contains the proof of a communication-complexity lower bound for near-neighbor search in L∞, matching the current upper bound of Piotr from FOCS'98. We were working on this problem during our summer internship at IBM Almaden (yes, yes, we're officemates but we had to go to California to write a paper together). As you might expect, the fact that we're now trying to finish the details has some correlation with the Nov 19 fireworks party :)

Here is my own contribution: a Starbucks napkin filled during a 2 hour caffeinated discussion with Alex. It contains the proof of a communication-complexity lower bound for near-neighbor search in L∞, matching the current upper bound of Piotr from FOCS'98. We were working on this problem during our summer internship at IBM Almaden (yes, yes, we're officemates but we had to go to California to write a paper together). As you might expect, the fact that we're now trying to finish the details has some correlation with the Nov 19 fireworks party :)

Friday, November 2, 2007
A Numbers Game
I have said before that I believe theory/CS is a numbers game. During a few discussions sub vino, I was challenged on this issue. Two main points seemed to emerge:
I have seen enough examples arguing for pessimism, mostly while I was acting as a reviewer. But since I can't actually talk about those, let me give 2 personal examples.
Predecessor. In STOC'06, Mikkel and I had our predecessor lower bound. The main claim to fame of this paper is that it was the first lower bound to separate linear and polynomial space.
When it comes to such a claim, in my opinion, it doesn't actually matter if you remember anything from the data structures class you took in college. It doesn't matter if you know that the bound is showing optimality of a very influential data structure from FOCS'75. It doesn't matter if you know this was one of the most well-studied problems in data-structure lower bounds, and people were actually betting the previous lower bound was tight.
No. Somebody comes and tells you that we've been toiling at this lower bound game for more than 20 years, and we haven't yet managed to show that a data structure with space n10 is sometimes better than one with space O(n). Now, they tell you, such a bound is finally here, and a vast array of problems from Algorithms 101 have switched from unapproachable to hopefully solvable. That should be a worthy result.
How did it feel from the inside? This was a paper we had worked on for 2 years. Just the conceptual understanding that we needed to develop felt like one of the longest journeys I have ever embarked on. And in the end, it was actually a clean result, which indeed needed conceptual developments, but not so much technical pain! Mikkel, who never ceases to amaze me with his youthful optimism, was betting on a best paper award. I was of course at a university, and had a better estimator of the community hype factor. I knew that Irit's PCP was unbeatable for an award, but I was still convinced our paper would go down with a splash.
The actual outcome? Moderately positive reviews. Nobody took notice. And we weren't even invited to the special issue, which was a genuine shock for us.
Range Counting. In STOC'07, I had a lower bound for 2D range counting. After the predecessor paper, I quickly decided this was the next big goal in the field. Range queries are very, very well-studied, play a crucial role in our understanding of data structures and geometry, and are a major bridge to worlds outside theory, such as databases (see this irrefutable argument). Armed with some appreciation of the techniques in the field, this also felt like a make-or-break problem: we were either going to solve it, or get stuck again for 20 years.
Though I like to look at cell-probe lower bounds, range counting has a life of its own. This class of problems was studied from the dawn of computer science, way before our understanding of models crystallized. People have been proving many excellent lower bounds for range queries in the so-called semigroup model: each input point is associated with weights from a semigroup; the goal is to compute the sum in a "range" (rectangle, circle, wizard's hat etc), using only the semigroup addition. In this model, we obtain a good understanding of geometry: it is enough to characterize a partial sum of a subset of points by the extreme points in a few directions. Addition only allows us to "build up" subsets, so we need to understand composability of constant-dimensional shapes, dictated by such extreme points.
While the bounds for semigroups were making very nice progress, we remained clueless about even the slightly stronger group model, where subtractions are allowed. This is the gap between understanding low-dimensional geometry and understanding computation (a very high-dimensional, unstructured space, such as the n-dimensional space of linear combinations). Proving bounds in the group model became the first lower-bound question in the surveys of Pankaj Agarwal and Jeff Erickson. Thus, the group model seemed hard enough; never mind the cell-probe model, which is significantly stronger than a model with additions and subtractions.
About a year after predecessor (I had the final critical insight one week before STOC), I managed to show an optimal lower bound for 2D range counting in the cell-probe and (of course) the group model. Again, it does not seem to me like a paper where you need to be an expert to understand that something interesting is happening. Citing from the abstract:
Finally, the paper was not invited to the special issue. By this time, it was not something that had never crossed my mind; it was just a disappointment.
Conclusion. You should work on major open problems. If you solve them, it makes for papers which are reject-proof (well, almost). But don't count on that "one big result" plan, as you may be in for a nasty surprise. As a community, we are reliable enough to get some kind of average right, but we're not doing so well on L∞.
So when you get your first STOC/FOCS paper, go open the champagne or light up the cigar. You are officially part of the game. Now, it's time to play.
Next round: November 19.
- What matters is your best result (L∞).
- STOC/FOCS get 10-15 obvious accepts, and a heavy tail of competent papers, among which it's hard to choose. If we care about making STOC/FOCS a quality measure, why not accept just those 10-15 papers?
I have seen enough examples arguing for pessimism, mostly while I was acting as a reviewer. But since I can't actually talk about those, let me give 2 personal examples.
Predecessor. In STOC'06, Mikkel and I had our predecessor lower bound. The main claim to fame of this paper is that it was the first lower bound to separate linear and polynomial space.
When it comes to such a claim, in my opinion, it doesn't actually matter if you remember anything from the data structures class you took in college. It doesn't matter if you know that the bound is showing optimality of a very influential data structure from FOCS'75. It doesn't matter if you know this was one of the most well-studied problems in data-structure lower bounds, and people were actually betting the previous lower bound was tight.
No. Somebody comes and tells you that we've been toiling at this lower bound game for more than 20 years, and we haven't yet managed to show that a data structure with space n10 is sometimes better than one with space O(n). Now, they tell you, such a bound is finally here, and a vast array of problems from Algorithms 101 have switched from unapproachable to hopefully solvable. That should be a worthy result.
How did it feel from the inside? This was a paper we had worked on for 2 years. Just the conceptual understanding that we needed to develop felt like one of the longest journeys I have ever embarked on. And in the end, it was actually a clean result, which indeed needed conceptual developments, but not so much technical pain! Mikkel, who never ceases to amaze me with his youthful optimism, was betting on a best paper award. I was of course at a university, and had a better estimator of the community hype factor. I knew that Irit's PCP was unbeatable for an award, but I was still convinced our paper would go down with a splash.
The actual outcome? Moderately positive reviews. Nobody took notice. And we weren't even invited to the special issue, which was a genuine shock for us.
Range Counting. In STOC'07, I had a lower bound for 2D range counting. After the predecessor paper, I quickly decided this was the next big goal in the field. Range queries are very, very well-studied, play a crucial role in our understanding of data structures and geometry, and are a major bridge to worlds outside theory, such as databases (see this irrefutable argument). Armed with some appreciation of the techniques in the field, this also felt like a make-or-break problem: we were either going to solve it, or get stuck again for 20 years.
Though I like to look at cell-probe lower bounds, range counting has a life of its own. This class of problems was studied from the dawn of computer science, way before our understanding of models crystallized. People have been proving many excellent lower bounds for range queries in the so-called semigroup model: each input point is associated with weights from a semigroup; the goal is to compute the sum in a "range" (rectangle, circle, wizard's hat etc), using only the semigroup addition. In this model, we obtain a good understanding of geometry: it is enough to characterize a partial sum of a subset of points by the extreme points in a few directions. Addition only allows us to "build up" subsets, so we need to understand composability of constant-dimensional shapes, dictated by such extreme points.
While the bounds for semigroups were making very nice progress, we remained clueless about even the slightly stronger group model, where subtractions are allowed. This is the gap between understanding low-dimensional geometry and understanding computation (a very high-dimensional, unstructured space, such as the n-dimensional space of linear combinations). Proving bounds in the group model became the first lower-bound question in the surveys of Pankaj Agarwal and Jeff Erickson. Thus, the group model seemed hard enough; never mind the cell-probe model, which is significantly stronger than a model with additions and subtractions.
About a year after predecessor (I had the final critical insight one week before STOC), I managed to show an optimal lower bound for 2D range counting in the cell-probe and (of course) the group model. Again, it does not seem to me like a paper where you need to be an expert to understand that something interesting is happening. Citing from the abstract:
Proving such bounds in the group model has been regarded as an important challenge at least since [Fredman, JACM 1982] and [Chazelle, FOCS 1986].It seems to me that whenever somebody claims to address a challenge from JACM'82 and FOCS'86, the only possible answers are:
- You are lying.
- The paper is wrong.
- It seemed like an interesting problem back then, but things have changed and we no longer care. (... and I don't see this applying to range queries.)
- Yes, this is a very good paper.
Finally, the paper was not invited to the special issue. By this time, it was not something that had never crossed my mind; it was just a disappointment.
Conclusion. You should work on major open problems. If you solve them, it makes for papers which are reject-proof (well, almost). But don't count on that "one big result" plan, as you may be in for a nasty surprise. As a community, we are reliable enough to get some kind of average right, but we're not doing so well on L∞.
So when you get your first STOC/FOCS paper, go open the champagne or light up the cigar. You are officially part of the game. Now, it's time to play.
Next round: November 19.
Sunday, October 28, 2007
Rational Search
We all know the number guessing game. I think of an integer between 1 and n, and you try to guess it by comparison queries, "is it larger than x?". Binary search takes ceiling(log2 n) queries, which is of course optimal.
But what if I think of a rational number a/b , with 0<a<b<n? Can you still guess it with a few comparison queries? Take a few seconds to show that you can guess it with 2log2 n + O(1) queries, and that's optimal. (It's a 1-line proof.)
x
x
x
x
x
x
This space intentionally left blank.
x
x
x
x
x
x
Two fractions with denominators up to n cannot be closer than 1/n2. Thus, you binary search for k such that the number is in the interval [k/n2 , (k+1)/n2). This interval contains a single fraction, so you can just go through all fractions and find the one inside. On the lower-bound side, there are on the order of n2 fractions, so it takes at least 2log2 n - O(1) queries with binary output.
The moral of the story is, of course: be careful about the difference between actual running time and query complexity. But now let us show that you can actually find the unique fraction in the small interval with running time O(lg n). There are several papers doing this, including:
The really cool property of irreducible fractions is that if a/b and c/d are consecutive in some Farey sequence, then the "mediant" (a+b)/(c+d) is the first fraction that appears between them in a higher-order sequence. For example, the first fraction to appear between 1/2 and 2/3 will be 3/5.
With this property, we can construct the Stern-Brocot tree, which is an infinite tree exploring all fractions less than 1. The following picture from Wikipedia should explain everything:
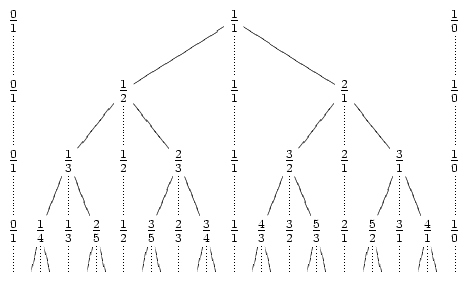 The intuitive algorithm is to go down this tree, looking for our fraction. Unfortunately, fractions with small denominators can appear very deep in the tree -- for example, 1/n is at depth n-1. Thus, we get O(n) time.
The intuitive algorithm is to go down this tree, looking for our fraction. Unfortunately, fractions with small denominators can appear very deep in the tree -- for example, 1/n is at depth n-1. Thus, we get O(n) time.
To improve this, we first show that the number of "turns" of the exploration is at most O(lg n). By turn, I mean switching from a going down on left children, to going down on right children (note that the 1/n example above had zero turns). Looking at the tree, it is easy to see that a turn essentially doubles denominators, so the property is easy to show.
Now we have to explore the straight descents efficiently. Let's say the fraction falls between a/b and c/d, and we take t steps to the left. This will land us at precisely (ta+b)/(tc+d). We can solve this equation for t, and find the minimum value which makes the fraction less than the target interval. Thus, we can calculate the number of consecutive left steps in constant time.
If we're too lazy to solve the equation, we can binary-search for t. Here we use galopping binary search, i.e. we take time O(lg t) to guess the unknown t.
Surprisingly, this will not give O(lg2n) time in total, but still takes O(lg n) time. This follows because the sum of the lg t values traces the number of times the denominator doubles, and it can only double O(lg n) times.
Overall, we have query complexity, Farey sequences, doubling arguments, galopping binary search, and summing up logarithms. This probably makes very nice material for an undergraduate "Math for CS" course.
(As a person who has never taken, nor taught such a course, I of course feel entitled to have opinions about it.)
But what if I think of a rational number a/b , with 0<a<b<n? Can you still guess it with a few comparison queries? Take a few seconds to show that you can guess it with 2log2 n + O(1) queries, and that's optimal. (It's a 1-line proof.)
x
x
x
x
x
x
This space intentionally left blank.
x
x
x
x
x
x
Two fractions with denominators up to n cannot be closer than 1/n2. Thus, you binary search for k such that the number is in the interval [k/n2 , (k+1)/n2). This interval contains a single fraction, so you can just go through all fractions and find the one inside. On the lower-bound side, there are on the order of n2 fractions, so it takes at least 2log2 n - O(1) queries with binary output.
The moral of the story is, of course: be careful about the difference between actual running time and query complexity. But now let us show that you can actually find the unique fraction in the small interval with running time O(lg n). There are several papers doing this, including:
- Christos Papadimitriou, Efficient search for rationals, IPL 1979.
- Steven P. Reiss, Efficient search for rationals, IPL 1979
- Stephen Kwek and Kurt Mehlhorn, Optimal Search for Rationals, IPL 2003.
The really cool property of irreducible fractions is that if a/b and c/d are consecutive in some Farey sequence, then the "mediant" (a+b)/(c+d) is the first fraction that appears between them in a higher-order sequence. For example, the first fraction to appear between 1/2 and 2/3 will be 3/5.
With this property, we can construct the Stern-Brocot tree, which is an infinite tree exploring all fractions less than 1. The following picture from Wikipedia should explain everything:
 The intuitive algorithm is to go down this tree, looking for our fraction. Unfortunately, fractions with small denominators can appear very deep in the tree -- for example, 1/n is at depth n-1. Thus, we get O(n) time.
The intuitive algorithm is to go down this tree, looking for our fraction. Unfortunately, fractions with small denominators can appear very deep in the tree -- for example, 1/n is at depth n-1. Thus, we get O(n) time.To improve this, we first show that the number of "turns" of the exploration is at most O(lg n). By turn, I mean switching from a going down on left children, to going down on right children (note that the 1/n example above had zero turns). Looking at the tree, it is easy to see that a turn essentially doubles denominators, so the property is easy to show.
Now we have to explore the straight descents efficiently. Let's say the fraction falls between a/b and c/d, and we take t steps to the left. This will land us at precisely (ta+b)/(tc+d). We can solve this equation for t, and find the minimum value which makes the fraction less than the target interval. Thus, we can calculate the number of consecutive left steps in constant time.
If we're too lazy to solve the equation, we can binary-search for t. Here we use galopping binary search, i.e. we take time O(lg t) to guess the unknown t.
Surprisingly, this will not give O(lg2n) time in total, but still takes O(lg n) time. This follows because the sum of the lg t values traces the number of times the denominator doubles, and it can only double O(lg n) times.
Overall, we have query complexity, Farey sequences, doubling arguments, galopping binary search, and summing up logarithms. This probably makes very nice material for an undergraduate "Math for CS" course.
(As a person who has never taken, nor taught such a course, I of course feel entitled to have opinions about it.)
Thursday, October 11, 2007
Range Queries (I)
I am now in Bonn, spending some time talking to Yakov Nekritch about range queries. Since this is a field I care about a lot, I will write a series of posts on it.
First, let me begin with my spiel on the importance of studying range queries. This is taken from the beginning of my talk at UW in May.
Once upon a time, you go to a bar in NY and you're trying to pick up a nice woman. She tells you she works in HR, and you tell her you are a theoretical computer scientist. She confesses she has not idea what that means, at which point you clarify "Oh, I am trying to understand the fundamental nature of computation". The blank stare you get is a clear indication that some more clarification is needed.
What do you then explain at this crucial moment of the night? Though I have not tried the following options myself, the prevailing opinion is that they are ill-advised:
But here you're in luck. The gorgeous HR woman actually uses computers every day, and she knows exactly what they're supposed to do. Chances are, she even has some exposure to a programming language! That is of course SQL, which is very useful for her work. The only trouble is -- for her, and for most of the planet, computers are a great tool for data storage and manipulation, not a great tool for finding Hamiltonian paths.
So what do you tell her? Anybody who has attended 5 minutes of a SQL tutorial has seen examples like:
You can now explain that your work is about how fast such queries can be executed, and, with her curiosity satisfied, move to more charming topics.
PS: This post is not about bad-mouthing complexity theory. For a long time, I have considered myself a complexity theorist, and I am interested in many topics in the field, well beyond my own research. The funny references are to some very particular young-and-eager complexity theorists, who have occasionally exasperated me with comments like "Yeap, data structures can be interesting sometimes, but really our goal is to understand computation". The point, if it was not clear enough, is that data structures are certainly not more artificial as our other computational questions -- maybe most computational questions that computer users care about are data-structure (database) questions.
First, let me begin with my spiel on the importance of studying range queries. This is taken from the beginning of my talk at UW in May.
Once upon a time, you go to a bar in NY and you're trying to pick up a nice woman. She tells you she works in HR, and you tell her you are a theoretical computer scientist. She confesses she has not idea what that means, at which point you clarify "Oh, I am trying to understand the fundamental nature of computation". The blank stare you get is a clear indication that some more clarification is needed.
What do you then explain at this crucial moment of the night? Though I have not tried the following options myself, the prevailing opinion is that they are ill-advised:
- I am trying to prove lower bounds for constant depth circuits with mod-6 gates.
- I am trying to extract pure randomness from 2 independent sources with small min entropy.
- I am trying to design codes of subexponential size with efficient local decodability.
- I am trying to show that a diagonalization argument cannot separate P and NP, even if it is given a low degree extension of an oracle.
But here you're in luck. The gorgeous HR woman actually uses computers every day, and she knows exactly what they're supposed to do. Chances are, she even has some exposure to a programming language! That is of course SQL, which is very useful for her work. The only trouble is -- for her, and for most of the planet, computers are a great tool for data storage and manipulation, not a great tool for finding Hamiltonian paths.
So what do you tell her? Anybody who has attended 5 minutes of a SQL tutorial has seen examples like:
In fact, she probably runs code like this on a daily basis. Thus, she already understands orthogonal range queries -- formally, you are given a set of points, and you ask for points in some rectangle.SELECT * FROM employees
WHERE salary <= 70000 AND startdate <= 1998
You can now explain that your work is about how fast such queries can be executed, and, with her curiosity satisfied, move to more charming topics.
PS: This post is not about bad-mouthing complexity theory. For a long time, I have considered myself a complexity theorist, and I am interested in many topics in the field, well beyond my own research. The funny references are to some very particular young-and-eager complexity theorists, who have occasionally exasperated me with comments like "Yeap, data structures can be interesting sometimes, but really our goal is to understand computation". The point, if it was not clear enough, is that data structures are certainly not more artificial as our other computational questions -- maybe most computational questions that computer users care about are data-structure (database) questions.
Friday, October 5, 2007
Schedule
For the past two weeks, I have been enjoying the unique atmosphere of Romania. I promise to blog a bit about Romania and its universities next week, since most people are probably not aware of this parallel academic universe.
Now it is time to get back into the real world, and possibly do some work. Of course, on the way to doing work, I might as well have some fun. My upcoming schedule is as follows:
Now it is time to get back into the real world, and possibly do some work. Of course, on the way to doing work, I might as well have some fun. My upcoming schedule is as follows:
- Oct 6: Timisoara (my first visit to this reportedly beautiful city in West Romania)
- Oct 7: Budapest
- Oct 8: Bratislava (first time in Slovakia)
- Oct 9: Amsteram
- Oct 10 -- Oct 16: Bonn
I am visiting Yakov Nekritch, whose homepage picture reminds me of pre-1989 Romania (a mid-level Party administrator for agriculture, looking proud of his crops).
On Monday, Oct 15, at 10am, I am giving the following talk:
Dynamic Graph Algorithms invade Geometry
After dynamic graph algorithms has been an area of intense research in data structures for almost 30 years, the time seems ripe for the field to tackle problems of a geometric nature. In dynamic graph algorithms, we have a graph that is being changed through updates (typically edge insertions and deletions), and we want to query it for various graph properties (say, whether two nodes are connected, the cost of an MST, the shortest path between two nodes etc).
Now consider a scenario in which we have sensors distributed in the space, and each sensor can only talk to another sensor at radius r. The connectivity is defined by the intersection graph of discs of radius r/2 around every point. Can we handle a dynamic environment, e.g. a situation when new sensors can be inserted, or some sensors run
out of battery?
Our results apply to the intersection graphs of a very general class of objects (includings disks, segments, rectangles) and support the dynamic connectivity problem in time O(nc) per update and query, where c is a constant less than 1 depending on the geometric shape in question. This opens a very broad and promising research direction:- can new graph queries be supported (e.g. shortest path queries)?
- what is the best running time for each important geometric shape?
Joint work with Timothy Chan and Liam Roditty. - Oct 16 -- Oct 20: Brussels (first time in Belgium)
Here, I am visiting Stefan Langerman. On Thrusday, Oct 18 at 12:30, I am giving a talk:
Farey Sequences and Counting Primitive Lattice Points
A primitive lattice point is a point (x,y) with x, y integers and gcd(x,y)=1. "Counting" primitive lattice points inside various planar shapes has been an active area of mathematics in the past decades. But by virtue of seeking an elementary formula, the mathematical definition of "counting" is "approximating asymptotically". We now present the first results on the informatics view of this problem: give an efficient algorithm to count primitive lattice points exactly.
The problem is related to another entertaining mathematical problem that has crossed the border into informatics. The Farey sequence of order N is the sorted sequence of irreducible fractions a/b, with a≤b≤N. There are well-known algorithms for generating this sequence in its entirety. We now describe algorithms for finding just one value of the sequence (say the K-th value) significantly faster.
Joint work with Jakub Pawlewicz. - Oct 20 -- Oct 23: FOCS in Providence.
The talk is on Monday morning at 8:30, and I am giving it (Mikkel and I use the alternation principle for choosing the speaker). The paper is here.
Planning for Fast Connectivity Updates
Understanding how a single edge deletion can affect the connectivity of a graph amounts to finding the graph bridges. But when faced with d>1 deletions, can we establish as easily how the connectivity changes? When planning for an emergency, we want to understand the structure of our network ahead of time, and respond swiftly when an emergency actually happens.
We describe a linear-space representation of graphs which enables us to determine how a batch of edge updates can impact the graph. Given a set of d edge updates, in time O(d.polylgn) we can obtain the number of connected components, the size of each component, and a fast oracle for answering connectivity queries in the updated graph. The initial representation is polynomial-time constructible.
Tuesday, October 2, 2007
CRA Award
In 2005, I received CRA's Outstanding Undergraduate Award (my citation, with a nicely kempt picture).
I have been asked a bunch of times (most recently yesterday) for "insider" tips, my nomination materials, opinions etc. So why not post all of these publicly on the blog, to promote competition...
Here is the research statement and the CV that I submitted back then (2004). It's nice to see the CV has changed a bit since then, not only in the contact info section ;)
Below is some "advice" and personal opinions that I wrote in emails. But there is a catch that you must be aware of -- I certainly did not have a typical application. I had a bunch of research even back then, and I got the award based on work in my sophomore year, which is very very atypical. Thus, you can either think that (1) the application was good enough to earn me the award so early, so my advice is trustworthy; or (2) my circumstances were sufficiently weird that the application didn't really matter, so my advice is worthless.
For what it's worth it, here was the formula I used:
Still, the fact that I did not speculate on future impact was probably the right thing to do. As I said already, I believe the tone of a statement at the student level should be strongly objective.
I have been asked a bunch of times (most recently yesterday) for "insider" tips, my nomination materials, opinions etc. So why not post all of these publicly on the blog, to promote competition...
Here is the research statement and the CV that I submitted back then (2004). It's nice to see the CV has changed a bit since then, not only in the contact info section ;)
Below is some "advice" and personal opinions that I wrote in emails. But there is a catch that you must be aware of -- I certainly did not have a typical application. I had a bunch of research even back then, and I got the award based on work in my sophomore year, which is very very atypical. Thus, you can either think that (1) the application was good enough to earn me the award so early, so my advice is trustworthy; or (2) my circumstances were sufficiently weird that the application didn't really matter, so my advice is worthless.
For what it's worth it, here was the formula I used:
- I got the advice (maybe it was even official advice from CRA) to describe carefully what my contribution was on the papers, so I do that to some extent in the statement. At a later stage in life (post PhD), this would probably be unusual.
- I was also told that some contribution to humanity might not hurt, so the CV emphasized my involvement in organizing high school computer olympiads. Still I decided not to dramatize it too much.
- I did not mention intended future work, broader impact, and the like. My reasoning was that empty talk is a skill that senior researchers need to develop for grants. It is understood that empty talk is needed, so including it will not hurt your reputation.
But if young students write the kind of things we normally write in grants, they end up looking sily and childish. They should compete based on objective things they actually did, and get some respect based on objective criteria before the hype can begin.
Still, the fact that I did not speculate on future impact was probably the right thing to do. As I said already, I believe the tone of a statement at the student level should be strongly objective.
Sunday, September 30, 2007
China (III)
I do not write about politics, since I could never be as good as some other people who do. A link to fellow theorist Bernard Chazelle, and the captivating essays on his webpage, is in order. (I hesitated posting a link not because I disagree with some of his arguments, which indeed I do, but because you will probably get distracted and not read the rest of my post... But render unto Caesar the things which are Caesar’s, I already said there are many people who write better than me.)
So, I did go to China, and I am back, and now I feel compelled to write a few words.
My friends in Romania ask me how the Chinese can stand their government, and why they are not fighting. Of course, the obvious guess on everybody's lips is panem et circenses -- the Chinese economy has been making strides forward, which allowed the government to keep citizens happy.

But another reason that cannot be ignored lies in the remarkable efficiency of Chinese propaganda among its citizens. A prime accomplishment of the communist machine is the fact that political discussion is so touchy among Chinese inteligentia in the US. The party has managed to convince even truly brilliant people that the state is the party and the party is the state. Then, if somebody challenges Chinese communism, they are attacking the Chinese patriotic sentiment. Love of the Vaterland becomes a shield of the regime.
Indeed, they are careful and proactive about propaganda. In the new age of communication, they have set up the world's best known firewall to keep the citizens away from subversive information. A non-technical person will not be able to get to Wikipedia, or to blogspot, or to any "unofficial" description of Tiananmen 1989, and will not be able to use encryption (ssh).
In fact, brainwashing and censorship were such a durable and effective efforts, that it became hard to get censors! A censor recently let a reference to Tiannmen be published because she thought June 4, 1989 was a mining disaster [Reuters].
Tiananmen has become the place where "On this spot in 1989, nothing happened".

Yet despite the brainwashing, there are those who are fighting (and currently losing). Taiwan's situation is constantly becoming worse, since every dollar that the booming Chinese economy earns is another dollar behind the economic blackmail in the One China policy. With Burkina Faso as the largest country to officially recognize Taiwan, their backing sadly reminds us of the grand Coalition of the Willing.
Inside the People's Republic, a cultural fight is led. In good Soviet tradition, the Party's policy was: grab as much land and people as possible, and rebrand everything as Chinese. (Han Chinese, of course.)
Tibet and Xinjiang are just about as Chinese as Finland. But in the past half-century, the Party has managed to bring 7 million or so Han into Xinjiang, a land populated by Turkic people (Uyghur and Kazakhs). This raised the percentage of Han from zeroish to 40%, and will soon make Xinjiang "Chinese", a feat that would have made the Father of Nations, Joseph Stalin, exceedingly proud.
As for Tibet, it may not even be needed to resort to ethnic invasion. Here is the simple story. The Dalai Lama and the Panchen Lama assure a continuity in Tibetan spiritual leadership. When one dies, the other searches for a reincarnation, and "takes care of business," while the young boy found to be the reincarnation grows up, and is educated to be a great Lama. When Panchen Lama died, the Dalai Lama (from exile in India) selected a new Panchen Lama in communication with a search commitee wandering across Tibet.
In 1995, the young boy became a political prisoner at the unlikely age of 6, and he has not been seen since. In its infinite wisdom and understanding of Tibetan culture, the Party chose the next Panchen Lama, and took the boy to Beijing. From there, he has been making periodic statements about the great freedom of religion enjoyed by the Chinese people living in Tibet.
Now, when the Dalai Lama dies, can anyone guess on what criteria the Panchen Lama (Beijing version) will select a reincarnation?
In the mean time, any attempt to cross into India and communicate with the Dalai Lama is a treason to the Chinese state. Here is a ghastly piece of footage caught by a Romanian cameraman while climbing in the Himalayas (which pedictably won some accolades at the Emmy Awards this year).
It shows a Chinese border patrol executing Tibetans who are trying to cross the mountain. Via the New York Times, we learn that China acknowledged the incident, and justified it as self-defense after the monks tried to attack the soldiers.
So, I did go to China, and I am back, and now I feel compelled to write a few words.
My friends in Romania ask me how the Chinese can stand their government, and why they are not fighting. Of course, the obvious guess on everybody's lips is panem et circenses -- the Chinese economy has been making strides forward, which allowed the government to keep citizens happy.

But another reason that cannot be ignored lies in the remarkable efficiency of Chinese propaganda among its citizens. A prime accomplishment of the communist machine is the fact that political discussion is so touchy among Chinese inteligentia in the US. The party has managed to convince even truly brilliant people that the state is the party and the party is the state. Then, if somebody challenges Chinese communism, they are attacking the Chinese patriotic sentiment. Love of the Vaterland becomes a shield of the regime.
Indeed, they are careful and proactive about propaganda. In the new age of communication, they have set up the world's best known firewall to keep the citizens away from subversive information. A non-technical person will not be able to get to Wikipedia, or to blogspot, or to any "unofficial" description of Tiananmen 1989, and will not be able to use encryption (ssh).
In fact, brainwashing and censorship were such a durable and effective efforts, that it became hard to get censors! A censor recently let a reference to Tiannmen be published because she thought June 4, 1989 was a mining disaster [Reuters].
Tiananmen has become the place where "On this spot in 1989, nothing happened".

Yet despite the brainwashing, there are those who are fighting (and currently losing). Taiwan's situation is constantly becoming worse, since every dollar that the booming Chinese economy earns is another dollar behind the economic blackmail in the One China policy. With Burkina Faso as the largest country to officially recognize Taiwan, their backing sadly reminds us of the grand Coalition of the Willing.
Inside the People's Republic, a cultural fight is led. In good Soviet tradition, the Party's policy was: grab as much land and people as possible, and rebrand everything as Chinese. (Han Chinese, of course.)
Tibet and Xinjiang are just about as Chinese as Finland. But in the past half-century, the Party has managed to bring 7 million or so Han into Xinjiang, a land populated by Turkic people (Uyghur and Kazakhs). This raised the percentage of Han from zeroish to 40%, and will soon make Xinjiang "Chinese", a feat that would have made the Father of Nations, Joseph Stalin, exceedingly proud.
As for Tibet, it may not even be needed to resort to ethnic invasion. Here is the simple story. The Dalai Lama and the Panchen Lama assure a continuity in Tibetan spiritual leadership. When one dies, the other searches for a reincarnation, and "takes care of business," while the young boy found to be the reincarnation grows up, and is educated to be a great Lama. When Panchen Lama died, the Dalai Lama (from exile in India) selected a new Panchen Lama in communication with a search commitee wandering across Tibet.
In 1995, the young boy became a political prisoner at the unlikely age of 6, and he has not been seen since. In its infinite wisdom and understanding of Tibetan culture, the Party chose the next Panchen Lama, and took the boy to Beijing. From there, he has been making periodic statements about the great freedom of religion enjoyed by the Chinese people living in Tibet.
Now, when the Dalai Lama dies, can anyone guess on what criteria the Panchen Lama (Beijing version) will select a reincarnation?
In the mean time, any attempt to cross into India and communicate with the Dalai Lama is a treason to the Chinese state. Here is a ghastly piece of footage caught by a Romanian cameraman while climbing in the Himalayas (which pedictably won some accolades at the Emmy Awards this year).
It shows a Chinese border patrol executing Tibetans who are trying to cross the mountain. Via the New York Times, we learn that China acknowledged the incident, and justified it as self-defense after the monks tried to attack the soldiers.
Thursday, September 20, 2007
Slepian, Wolf and relatives (III)
To wrap up this thread of posts, let me discuss some motivation and directions for asymmetric communication channels, described in post II.
In my talk in China, I mentioned the following naive motivation. We have two sensors in a river. Given the average velocity of the flow, we can deduce that the readings of the sensor upstream at some time t, will be correlated with the readings of the sensor downstream at some time t+Δt. The correlation will not be perfect (otherwise we wouldn't use two sensors), but it is enough to compress the message. However, the sensor downstream doesn't know the distribution of his own input, since he doesn't know the other sensor's reading at an earlier time.
This example is simple and intuitive enough that it should work as PR. Here are the more serious motivations that get thrown around:
Moving on to 2., I have not seen examples where this approach might be useful at the scale of realistic ISP links, nor examples of how you might get the server to know the distribution better than you.
About 3., I have a feeling that it is simply accidental cobranding. To get your paper accepted to a practical conference, it helps to use some fancy theoretical work somewhere (maybe a place where you don't even need it), and theoretical work can claim practical importance if somebody uses it in a supposedly practical conference. I am reminded of a funny quote: "I would gladly work on the practical side of academia, but so little of practice actually applies to practice..."
Thus, unfortunately, I do not find the motivations I heard so compelling (outside of theoretical beauty with which I will fully agree).
What is probably needed is more attention towards the EE end of the discipline. Is anybody aware of any EE-work on this problem? In our abstract setting (Bob knows a distribution), any algorithm is ultimately impractical, because nobody works with perfect knowledge of a distribution (a distribution is a big object!). What we need is better modelling of what "understanding a distribution" means, and algorithms based on that. To give the prototypical sily example, the distribution may be (roughly) normal, so Bob only needs to know the mean and standard deviation.
On the lower bound side, I have some rough ideas to prove that the lower bound holds even if the distribution is the trajectory of a Markov chain of polynomal size (as opposed to the distribution in our paper, which really took exponentially many bits to describe).
In my talk in China, I mentioned the following naive motivation. We have two sensors in a river. Given the average velocity of the flow, we can deduce that the readings of the sensor upstream at some time t, will be correlated with the readings of the sensor downstream at some time t+Δt. The correlation will not be perfect (otherwise we wouldn't use two sensors), but it is enough to compress the message. However, the sensor downstream doesn't know the distribution of his own input, since he doesn't know the other sensor's reading at an earlier time.
This example is simple and intuitive enough that it should work as PR. Here are the more serious motivations that get thrown around:
- sensor networks (in some abstract way)
- internet connections (most ISPs give you faster download than upload; downloading from a satellite is significantly easier than uploading)
- stenography and combating consorship. This comes from the paper: [Feamster, Balazinska, Harfst, Balakrishnan, Karger: Infranet: Circumventing Web Censorship and Surveillance. USENIX Security Symposium 2002]
Moving on to 2., I have not seen examples where this approach might be useful at the scale of realistic ISP links, nor examples of how you might get the server to know the distribution better than you.
About 3., I have a feeling that it is simply accidental cobranding. To get your paper accepted to a practical conference, it helps to use some fancy theoretical work somewhere (maybe a place where you don't even need it), and theoretical work can claim practical importance if somebody uses it in a supposedly practical conference. I am reminded of a funny quote: "I would gladly work on the practical side of academia, but so little of practice actually applies to practice..."
Thus, unfortunately, I do not find the motivations I heard so compelling (outside of theoretical beauty with which I will fully agree).
What is probably needed is more attention towards the EE end of the discipline. Is anybody aware of any EE-work on this problem? In our abstract setting (Bob knows a distribution), any algorithm is ultimately impractical, because nobody works with perfect knowledge of a distribution (a distribution is a big object!). What we need is better modelling of what "understanding a distribution" means, and algorithms based on that. To give the prototypical sily example, the distribution may be (roughly) normal, so Bob only needs to know the mean and standard deviation.
On the lower bound side, I have some rough ideas to prove that the lower bound holds even if the distribution is the trajectory of a Markov chain of polynomal size (as opposed to the distribution in our paper, which really took exponentially many bits to describe).
Wednesday, September 19, 2007
Slepian, Wolf and relatives (II)
I didn't really get the answers I was hoping for in my original post on Slepian-Wolf coding, but let's move to the second part.
This post is about "asymmetric communication channels". Assume Alice receives an input x in {0,1}n, and she wants to communicate it to Bob. If x comes from some distribution D of less with entropy less than n, Alice and Bob should agree to communicate using a Huffman code and send ≤ H(D)+1 bits.
But what if D is only known to Bob, and not to Alice? Can Bob send something intelligent, which is still much less than the 2n description of the distribution, but which allows Alice to communicate efficiently? If you want to hear motivations and applications of this setup, I will discuss them in my next post. Personally, I find this "can you communicate a Huffman code" question sufficiently natural and intriguing.
It is not hard to show that the total communication needs to be at least n. Thus, a nontrivial protocol is only possible in an asymmetric setting, where Bob is allowed to communicate more than Alice.
Upper bounds. The problem was first studied by Adler and Maggs [FOCS'98], who gave a protocol in which Bob sends expected O(n) bits, and Alice sends expected O(H) bits. This is a surprising result: Bob is sending some sketch of the distribution that is logarithmic in its description, but with this sketch Alice can compress her input down to entropy.
There is one catch, though: the protocol uses O(1) rounds in expectation. It does not provide a guarantee for any fixed number of rounds.
With this catch, you can start to get a glimpse of how the protocol might run. Up to constant factors, a distribution with entropy H looks like a distribution putting probability 2-(H+1) on some 2H samples (mass 1/2), then probability 2-(H+2) on other 2H samples (total mass 1/4), probability 2-(H+3) on other 2H samples (mass 1/8) and so on. Bob is going to send a hash function {0,1}n -> {0,1}H which is injective on the 2H samples on the first level, and Alice returns the hash code. Bob sends the sample that maps to that hash code, and if Alice says he was wrong, they continue to the second level (which will only happen with probability 1/2). This continues, reaching level i (and round i) with probability 2-O(i).
There has been a lot of follow-up work, which tries to reduce the constants in the communication. Some papers have Alice communicating only H+2 bits, for instance. However, I do not like these results because they use roughly H rounds in expectation. In real life, a round of communication is much much more expensive than sending a few extra bits.
In SODA'05, Adler extended the protocol to the case where there are k Alice's, which have samples x1, ..., xk to communicate. These samples come from a joint distribution, known only to Bob.
Lower bounds. Micah Adler came to a problem session organized by Erik, and told us about the problem, highlighting the weird behavior that the number of rounds is geometric. Personally, I was fascinated by the question of whether this was tight.
Unfortunately, the proof eventually required not only some nice ideas, but also a lot of work in balancing everything just right. I spent a few months paying long daily visits to Nick's office, before we finally managed to make it go through. In the slides for my talk in China, I associated this problem with a bas-relief depicting galley slaves.
The proof uses round elimination and message switching (which I will talk about in future posts), but in an unusual context: you need to keep recursing in these smaller and smaller probability spaces.
Eventually, we showed that i rounds are needed with probability 2-O(i lg i), which is fairly close to optimal, and demonstrates that any fixed number of rounds is not enough. In the good tradition of sharp phase transitions, the lower bound holds even if Bob can communicate an outrageous amount: 2^{n1-ε}.
Our paper appeared in SODA'06. The paper and slides have fairly good intuition for how the bound works.
This post is about "asymmetric communication channels". Assume Alice receives an input x in {0,1}n, and she wants to communicate it to Bob. If x comes from some distribution D of less with entropy less than n, Alice and Bob should agree to communicate using a Huffman code and send ≤ H(D)+1 bits.
But what if D is only known to Bob, and not to Alice? Can Bob send something intelligent, which is still much less than the 2n description of the distribution, but which allows Alice to communicate efficiently? If you want to hear motivations and applications of this setup, I will discuss them in my next post. Personally, I find this "can you communicate a Huffman code" question sufficiently natural and intriguing.
It is not hard to show that the total communication needs to be at least n. Thus, a nontrivial protocol is only possible in an asymmetric setting, where Bob is allowed to communicate more than Alice.
Upper bounds. The problem was first studied by Adler and Maggs [FOCS'98], who gave a protocol in which Bob sends expected O(n) bits, and Alice sends expected O(H) bits. This is a surprising result: Bob is sending some sketch of the distribution that is logarithmic in its description, but with this sketch Alice can compress her input down to entropy.
There is one catch, though: the protocol uses O(1) rounds in expectation. It does not provide a guarantee for any fixed number of rounds.
With this catch, you can start to get a glimpse of how the protocol might run. Up to constant factors, a distribution with entropy H looks like a distribution putting probability 2-(H+1) on some 2H samples (mass 1/2), then probability 2-(H+2) on other 2H samples (total mass 1/4), probability 2-(H+3) on other 2H samples (mass 1/8) and so on. Bob is going to send a hash function {0,1}n -> {0,1}H which is injective on the 2H samples on the first level, and Alice returns the hash code. Bob sends the sample that maps to that hash code, and if Alice says he was wrong, they continue to the second level (which will only happen with probability 1/2). This continues, reaching level i (and round i) with probability 2-O(i).
There has been a lot of follow-up work, which tries to reduce the constants in the communication. Some papers have Alice communicating only H+2 bits, for instance. However, I do not like these results because they use roughly H rounds in expectation. In real life, a round of communication is much much more expensive than sending a few extra bits.
In SODA'05, Adler extended the protocol to the case where there are k Alice's, which have samples x1, ..., xk to communicate. These samples come from a joint distribution, known only to Bob.
Lower bounds. Micah Adler came to a problem session organized by Erik, and told us about the problem, highlighting the weird behavior that the number of rounds is geometric. Personally, I was fascinated by the question of whether this was tight.
Unfortunately, the proof eventually required not only some nice ideas, but also a lot of work in balancing everything just right. I spent a few months paying long daily visits to Nick's office, before we finally managed to make it go through. In the slides for my talk in China, I associated this problem with a bas-relief depicting galley slaves.
The proof uses round elimination and message switching (which I will talk about in future posts), but in an unusual context: you need to keep recursing in these smaller and smaller probability spaces.
Eventually, we showed that i rounds are needed with probability 2-O(i lg i), which is fairly close to optimal, and demonstrates that any fixed number of rounds is not enough. In the good tradition of sharp phase transitions, the lower bound holds even if Bob can communicate an outrageous amount: 2^{n1-ε}.
Our paper appeared in SODA'06. The paper and slides have fairly good intuition for how the bound works.
Job Market
Since I have announced that I am graduating this year and looking for a job, people have been asking me who else is on the market. I am in China now, with all the brilliant graduate students, so I took the opportunity to ask who will be on the job market. Here is the list of people who said they will be applying for faculty jobs in the US in 2007. This list does not include people who announced they are only looking for postdocs, or who want jobs outside US.
Alphabetically:
I have heard (rumours) about the following people:
Alphabetically:
- Nina Balcan
- Andrej Bogdanov
- Mark Braverman (maybe)
- Constantinos Daskalakis
- Nick Harvey
- Philipp Hertel (maybe)
- Adriana Karagiozova (maybe)
- Anup Rao (maybe)
- Paul Valiant
- Ryan Williams
- Amir Yehudayoff (maybe)
I have heard (rumours) about the following people:
Monday, September 17, 2007
China (II)
As announced, I am attending China Theory Week in Beijing.
Sadly, this puts me behind the Great Firewall of China, which hates blogspot. I will wait until I leave China to express my opinion on this :) Lots and lots of thanks to Erik and Elad Verbin (currently postdoc here), for teaching me how to get around the firewall.
My talk here was: "Round Elimination — A Proof, A Concept, A Direction."
If you know my usual style of giving talks, you know the slides are somewhat unorthodox. Since I will hopefully give a nonzero number of job talks in the spring, I am especially curious what readers think of the advice on slide 2 :)
Sadly, this puts me behind the Great Firewall of China, which hates blogspot. I will wait until I leave China to express my opinion on this :) Lots and lots of thanks to Erik and Elad Verbin (currently postdoc here), for teaching me how to get around the firewall.
My talk here was: "Round Elimination — A Proof, A Concept, A Direction."
Round elimination, which can be traced back to [Ajtai 1989], has proven to be one of the most useful tools in communication complexity, playing a role similar to PCPs in approximation algorithms. We describe the history of its many variants, including the simplest known proof, and the most illustrative applications. We also describe possible future work, including conjectures that would bring significant progress in applications.Slides are available in pptx or exported as ppt. The PDF didn't look decent enough to be posted; sorry.
Based on literature survey, and joint publications with Micah Adler, Amit Chakrabarti, Erik Demaine, Sudipto Guha, TS Jayram, Nick Harvey, and Mikkel Thorup.
If you know my usual style of giving talks, you know the slides are somewhat unorthodox. Since I will hopefully give a nonzero number of job talks in the spring, I am especially curious what readers think of the advice on slide 2 :)
Learn from Holywood: sex and violence are the key to a successful job talk.
Friday, September 14, 2007
Slepian, Wolf and relatives (I)
The [Splepian-Wolf'73] coding scheme is a famous result in coding theory, that inspired the field of distributed source coding. I guess this topic would be better for Michael's blog, but I am curious to ask some questions, and I want to describe a slightly related beast in the next post.
Review. You have k clients, and a server. The clients have some inputs x1, ..., xk, each of n bits, and they want to communicate all inputs to the server. Now assume these inputs come from some joint distribution with entropy much less than nk. Can one use similarly little communication?
If the distribution is rectangular, i.e. the xi's are independent, each client i can perform source coding (say, Huffman coding) based on his own distribution, achieving H(xi) communication. With dependencies, if clients broadcast their messages in order, each client can perform source coding based on his distribution conditioned on the previous messages. This achieves optimal total communication, since Sumi H(xi | x1, ..., xi-1) = H(x1, ..., xk).
Slepian and Wolf showed that it is possible to achieve optimal communication even if all clients communicate one message simmultaneously, and the messages are only seen by the server.
In fact, there is a whole simplex of possible scenarios for optimal communication. Consider k=2 to make notation easy. Then, it is possible for client 1 to send m1 bits, and client to to send m2 bits as long as:
Since then, people have developed efficently encodable and decodable distributed codes for all sorts of important special cases. A "special case" means what makes the inputs correlated (they are close in what metric?). To give realistic examples, the inputs may be close in Hamming distance, or in edit distance, or they may be numbers that are close in value (say, two noisy observations of the same event).
Questions. I never actually worked on this (but on something related, see next post), so I only have some meta questions. The field is usually sold as being important in sensor networks. Is this "for real", or just theoretical PR? People interested in sensor networks on our side of theory (eg the streaming folks) do not seem too aware or interested in this field. Why?
Review. You have k clients, and a server. The clients have some inputs x1, ..., xk, each of n bits, and they want to communicate all inputs to the server. Now assume these inputs come from some joint distribution with entropy much less than nk. Can one use similarly little communication?
If the distribution is rectangular, i.e. the xi's are independent, each client i can perform source coding (say, Huffman coding) based on his own distribution, achieving H(xi) communication. With dependencies, if clients broadcast their messages in order, each client can perform source coding based on his distribution conditioned on the previous messages. This achieves optimal total communication, since Sumi H(xi | x1, ..., xi-1) = H(x1, ..., xk).
Slepian and Wolf showed that it is possible to achieve optimal communication even if all clients communicate one message simmultaneously, and the messages are only seen by the server.
In fact, there is a whole simplex of possible scenarios for optimal communication. Consider k=2 to make notation easy. Then, it is possible for client 1 to send m1 bits, and client to to send m2 bits as long as:
- m1+m2 ≥ H(x1, x2)
- m1 ≥ H(x1 | x2)
- m2 ≥ H(x2 | x1)
Since then, people have developed efficently encodable and decodable distributed codes for all sorts of important special cases. A "special case" means what makes the inputs correlated (they are close in what metric?). To give realistic examples, the inputs may be close in Hamming distance, or in edit distance, or they may be numbers that are close in value (say, two noisy observations of the same event).
Questions. I never actually worked on this (but on something related, see next post), so I only have some meta questions. The field is usually sold as being important in sensor networks. Is this "for real", or just theoretical PR? People interested in sensor networks on our side of theory (eg the streaming folks) do not seem too aware or interested in this field. Why?
Athena and TCS
In the ancient days of radical democracy, Αθήνα was run by her people through direct involvement. The school of thought of this democracy held that the people governing themselves could not be wrong. The ἐκκλησία or Ήλιαία could not possibly judge wrongly, even when making impulsive decisions governed by mob mentality. Instead, if one of these institutions reached a decision shown later to be objectively wrong, it was because the people did not posses enough information at the time, or because they were misled.
In the scientific community (especially in theoretical branches), we are running our own experiment in radical democracy. We have essentially no outside constraints, no obligation to finish some research about some topic by some deadline. We are judging our own work, and allocating the resources among ourselves.
So if a PC rejects your paper, or NSF decides not to fund your grant proposal, you should be angry and make creative use of English adjectives over beer. But after this ritual dedicated to Πανάκεια, you should understand that your colleagues rejected your work not because they are ἰδιώτες (pun intended -- idiot originally meant people who were not involved in community decisions, preferring a private life), but because they didn't know better.
So give talks, lobby for your field over beer, write a 5-page introduction to every paper, or you know, maybe start a blog ;)
If the field really consists of narrow-minded people who permanently refuse to understand what you're talking about, you are in the wrong field.
In the scientific community (especially in theoretical branches), we are running our own experiment in radical democracy. We have essentially no outside constraints, no obligation to finish some research about some topic by some deadline. We are judging our own work, and allocating the resources among ourselves.
So if a PC rejects your paper, or NSF decides not to fund your grant proposal, you should be angry and make creative use of English adjectives over beer. But after this ritual dedicated to Πανάκεια, you should understand that your colleagues rejected your work not because they are ἰδιώτες (pun intended -- idiot originally meant people who were not involved in community decisions, preferring a private life), but because they didn't know better.
So give talks, lobby for your field over beer, write a 5-page introduction to every paper, or you know, maybe start a blog ;)
If the field really consists of narrow-minded people who permanently refuse to understand what you're talking about, you are in the wrong field.
3n+1
A vivid example that the halting problem is hard... :)
Is there some n for which the following algorithm does not halt?
Like many people I know, I too spent some time in high school trying to tackle it. Other people, who presumably spent quite a bit of time on the problem after high school, showed various interesting things. For example, if a cycle exists, it has size at least 275000 [Lagarias 85].
While this may look like a CS problem, I suggest we do not claim it, and let the mathematicians worry about it for a while.
Is there some n for which the following algorithm does not halt?
int n;Of course, this is the famous 3n+1 problem, or the Collatz problem. It dates back to 1937, and many people are betting that it's "the next Fermat", if it is lucky enough to stay unsolved for a few more centuries. Erdős said "Mathematics is not yet ready for such problems."
scanf("%d", &n);
while(n > 1)
n = (n % 2) ? 3*n+1 : n/2;
Like many people I know, I too spent some time in high school trying to tackle it. Other people, who presumably spent quite a bit of time on the problem after high school, showed various interesting things. For example, if a cycle exists, it has size at least 275000 [Lagarias 85].
While this may look like a CS problem, I suggest we do not claim it, and let the mathematicians worry about it for a while.
Monday, September 10, 2007
A word from our sponsors (I)
With the MIT tuition bill arriving, our IBMish paper being accepted to SODA, and Michael running a similar series, I figured it was high time to speak about money and sponsors.
I am pleased to announce that Erik and I sold our soul to Google this year, and in return won a Google Research Award. Our grant proposal was on "Fundamental Data Structures". If this didn't scare Google, they must be pretty open to foundational research, and any myth to the contrary seems outdated :)
Our proposal consisted of a list of some papers we wrote (together and separately), with a 3-line summary for each. We worked quite a bit on putting together the list, with the goal to extract an exclamation from any reader at one point or another. As usual, Erik is the perfect co-writer for any piece of text (it's a pity he won't do blogging...).
The same team (Erik as PI, and yours truly as "Senior Researcher") tried a similar stunt with NSF (different topic though), without success. The comments were a maximal set of strong and contradictory statements from a couple of panels.
My favorites (yes, I know you don't usually make this list public):
I am pleased to announce that Erik and I sold our soul to Google this year, and in return won a Google Research Award. Our grant proposal was on "Fundamental Data Structures". If this didn't scare Google, they must be pretty open to foundational research, and any myth to the contrary seems outdated :)
Our proposal consisted of a list of some papers we wrote (together and separately), with a 3-line summary for each. We worked quite a bit on putting together the list, with the goal to extract an exclamation from any reader at one point or another. As usual, Erik is the perfect co-writer for any piece of text (it's a pity he won't do blogging...).
The same team (Erik as PI, and yours truly as "Senior Researcher") tried a similar stunt with NSF (different topic though), without success. The comments were a maximal set of strong and contradictory statements from a couple of panels.
My favorites (yes, I know you don't usually make this list public):
- This is a very well-written proposal.
- My tendency is to recommend not to fund this proposal in order that the PIs write it better.
- Even the most optimistic progress will only [..] have little practical application.
- This is a highly important research direction that [..] will allow to develop more practically feasible geometric algorithms.
- What are the broader impacts of the proposed activity? None!
- Faster algorithms [..] might be much faster in practice. In fact, I believe that such improvements might lead to more practical and realistic algorithms.
- Very strong proposal - it's definitely not "more of the same" like many other proposals.
Sunday, September 9, 2007
SODA 2008 (updated)
The list of accepted papers has been posted.
If you get this weird feeling that something is missing, remember that he was on the PC.
On a rough count, there are about 13 data structure papers (cf. 16 last year), matching my prediction that the number of papers is not really affected by PC composition. From what I understand, most PCs are not actively trying to balance accept ratios across fields, so this phenomenon has a nonobvious explanation. (Maybe it is proof that the PC mechanism "works" in some abstract sense.)
I am also happy to report that our paper was accepted.
If you get this weird feeling that something is missing, remember that he was on the PC.
On a rough count, there are about 13 data structure papers (cf. 16 last year), matching my prediction that the number of papers is not really affected by PC composition. From what I understand, most PCs are not actively trying to balance accept ratios across fields, so this phenomenon has a nonobvious explanation. (Maybe it is proof that the PC mechanism "works" in some abstract sense.)
I am also happy to report that our paper was accepted.