The following simple puzzle was circulating among Romanian olympiad participants around 1998. It was supposed to be a quick way to tell apart algorithmists from mere programmers.
Given an undirected graph G, and two vertices u and v, find a cycle containing both u and v, or report than none exists. Running time O(m).
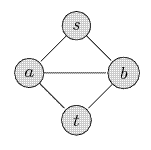
Update: Simple ideas based on a DFS (like: find one path, find another) do not work. Think of the following graph:
If you first find the path s → a → b → t, you will not find a second.
The one-line answer is: try to route two units on flow from s to t in the unit-capacity graph (with unit node capacities if you want simple cycles). This is not the same as two DFS searches, because the second DFS is in the residual graph (it can go back on the edges of the first DFS).
But how do you compute the optimal value for Alice? If the sum of even and odd is equal, how can Alice determine whether she can win, or only draw? A simple dynamic program running in O(n2) time works. Can you solve it faster?
16 comments:
single DFS from u. there is a cycle iff there is a whitepath to u from a node in the subtree of v.
yeah just backtrack through parents in DFS tree if v hit; if v not hit, no cycle. DFS times O(m), backtrack time O(m).
It seems to be straightforward flow with value 2. Am I right?
i was anon 2, who MISREAD.
corrected solution--DFS from u, backtrack after hitting v (through parents in tree) to find a u--v path. cut this path's edges from the graph, and DFS to find another path. works since undirected graph has cycle iff has pair of paths.
the 2-flow idea works too, in fact it'll do what i wrote (find a path, mark it as used, find another).
Do you want edge-disjoint/node-disjoint cycles?
Do you want edge-disjoint/node-disjoint cycles?
Doesn't matter, both have an O(m) solution.
An interesting variant would be find such a cycle in a directed graph.
An interesting variant would be find such a cycle in a directed graph.
But that is simply DFS, no?
Mihai, how do you define the residual graph for a flow problem with node capacities in an *undirected* graph?
Just trying to see if you are an mathematician, or a mere algorithmist. :)
What's wrong with the residual network for an undirected node-capacitated graph? It seems like a perfectly healthy creature to me. It's of course a directed graph.
Just define it. Let's say I have G=(V_G,E_G) undirected, with capacities u_G, and a flow x on it. What exactly is R=(V_R, E_R), and what are the capacities u_R?
Dude, you shouldn't run flow on the undirected graph if you want to add node capacities. Every node v is split into v1 and v2; all edge have a version coming into v1 and one going out of v2. There is a single edge between v1 and v2 with the capacity of the node. The residual network is just what the residual network is.
Ok, so let's look at your directed network (assume no node capacities for the moment).
Say you find a flow given by two paths v, v_1, v_2, ..., v_k, u
and v, w_1, w_2, ..., v_7, v_6, ..., v_3, v_2, ..., v_10, v_9, ..., w_l, u.
What next?
Ok, I think I understand your problem: you may get a flow plus a circulation, instead of just a flow.
0) Recap your lectures on flow :) These things have fairly standard fixes.
1) You can avoid the extra circulation by implementing your flow carefully. More precisely, the back edges in the residual graph should have priority in your 2nd run of DFS (this way, if there is a path going back on some edges, you will go back in a contiguous way, not hop on and off the back path).
2) Otherwise, you can easily get rid of the extra circulation. In the node-capacitated case, just keep the edges with nonzero flow that are in the same connected component with the source and sink.
Without node capacities, do two DFS from the source to the sink, staying only on edges with nonzero flow. The 2nd scan cannot get stuck, by flow conservation (what comes in must go out).
PS: You should really implement this (I did it in 98 or so). You will understand these technical details much better when you need to think of them carefully.
Post a Comment